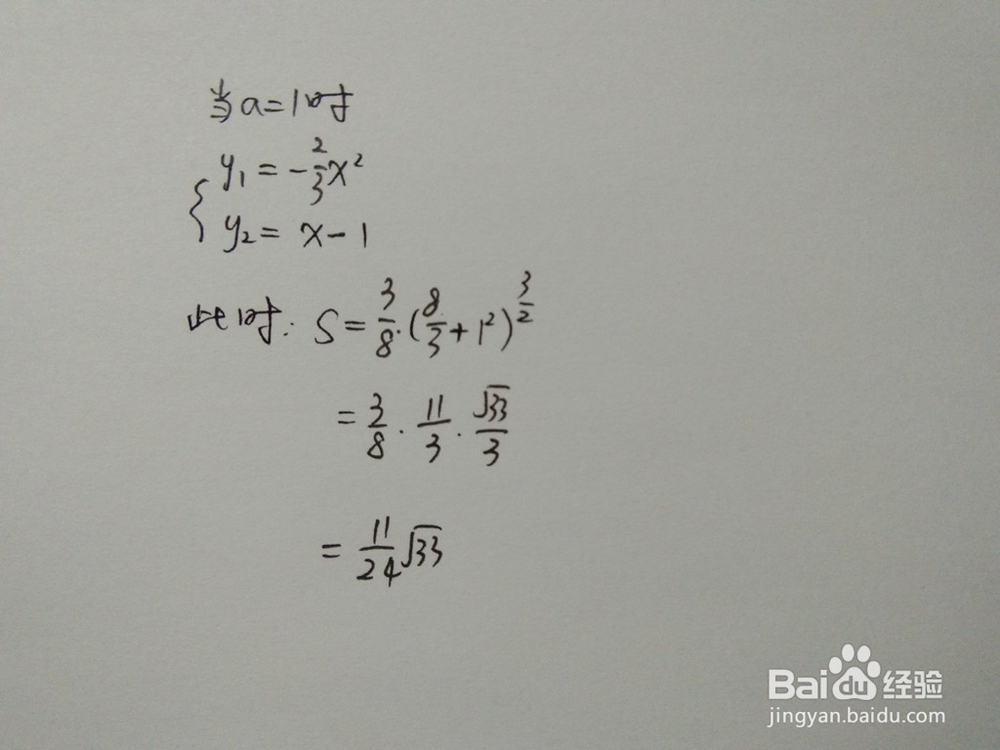本经验,通过定积分的知识,介绍曲线y1=-2x^2/3与直线y2=ax-1围成的面积的计算步骤,其中a=0,1/3,1/2,1.
工具/原料
二次函数相关知识
图像有关知识
1.围成面积通式推导
1、联立方程,求交点通式如下:
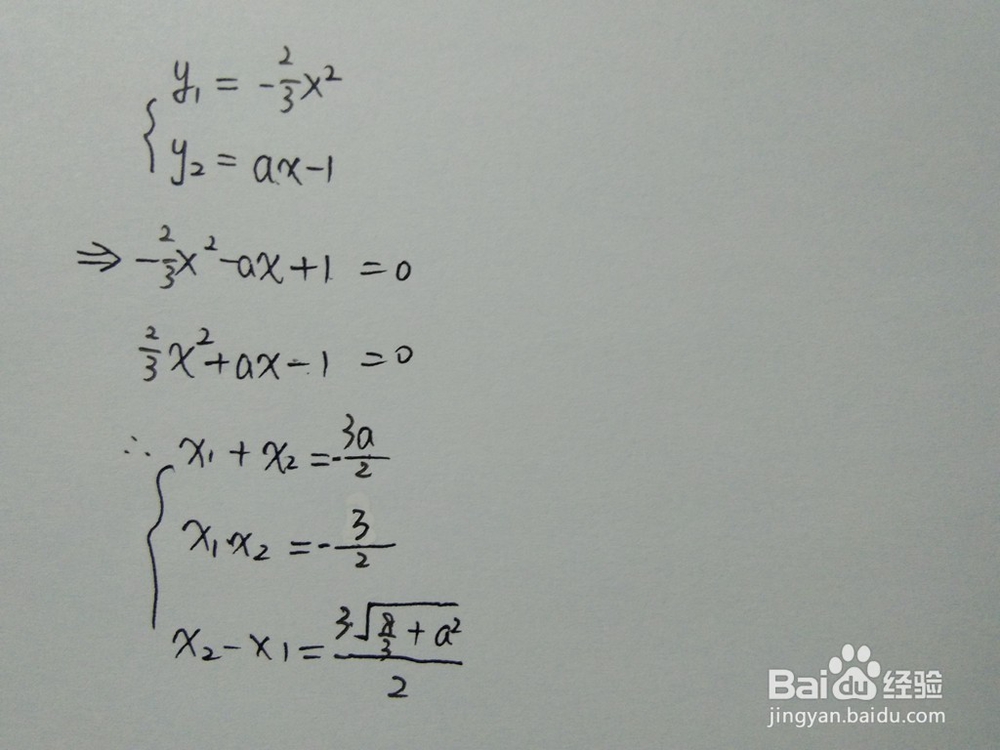
2、通过定积分,求围成面积通式如下:
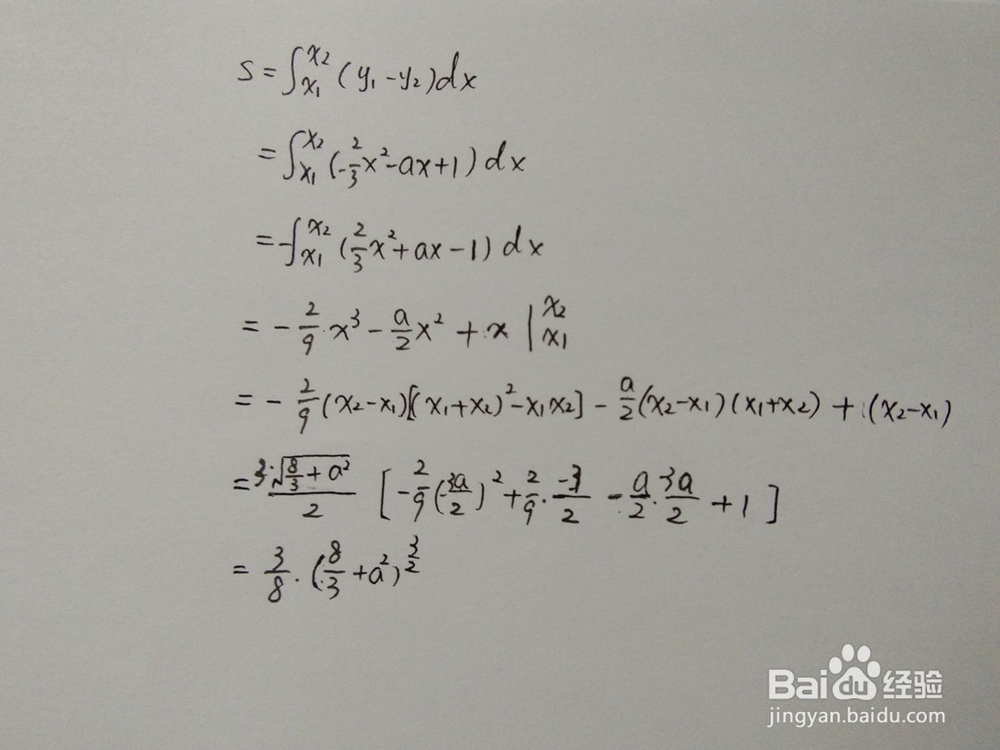
2.当a=0时
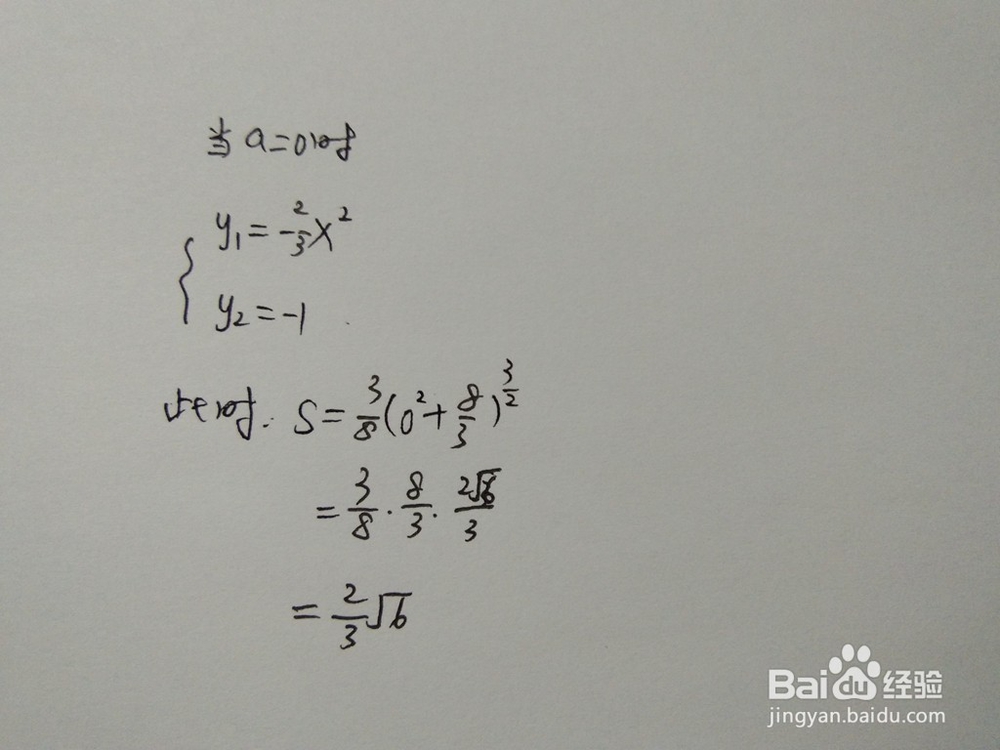
3.当a=1/3时
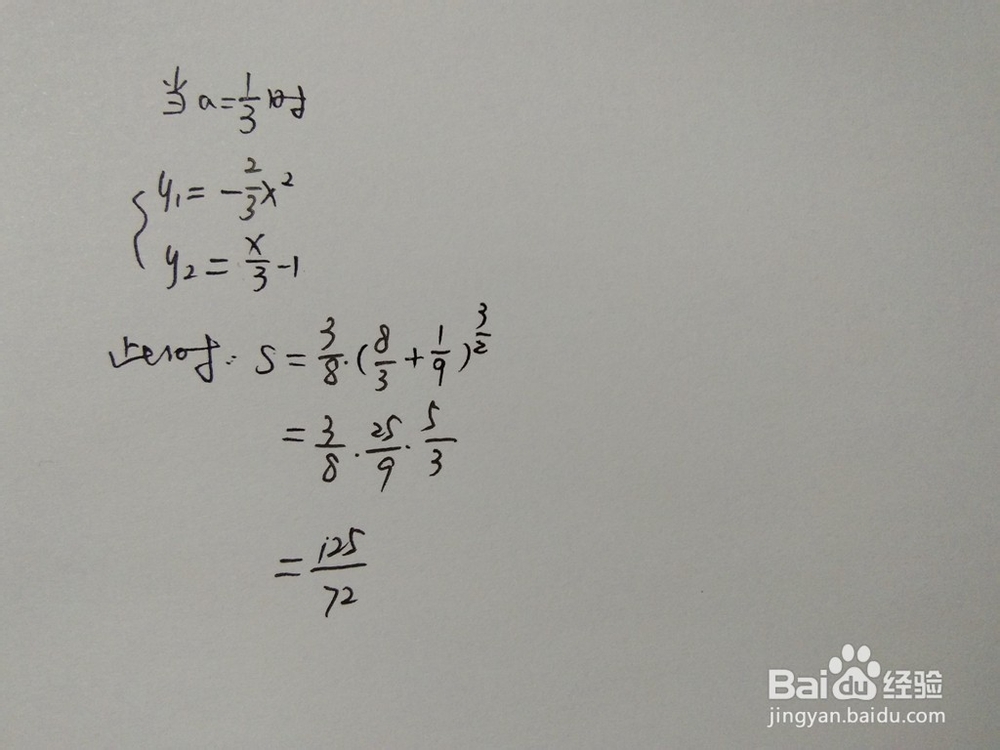
4.当a=1/2时

5.当a=1时
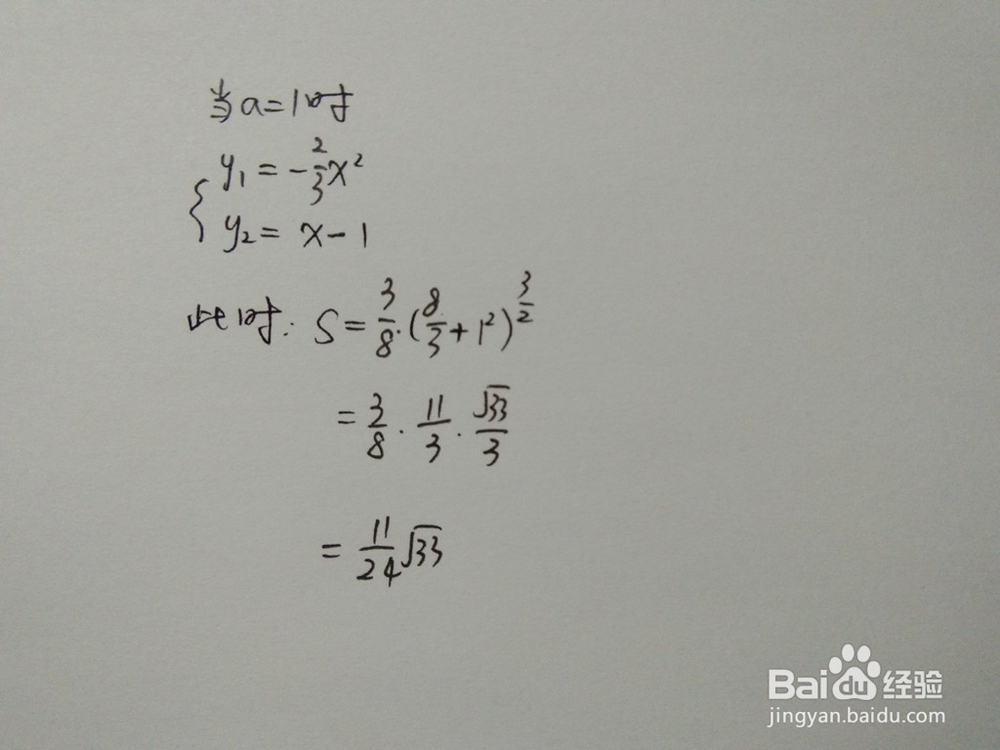
时间:2024-10-14 15:50:07
本经验,通过定积分的知识,介绍曲线y1=-2x^2/3与直线y2=ax-1围成的面积的计算步骤,其中a=0,1/3,1/2,1.
工具/原料
二次函数相关知识
图像有关知识
1.围成面积通式推导
1、联立方程,求交点通式如下:
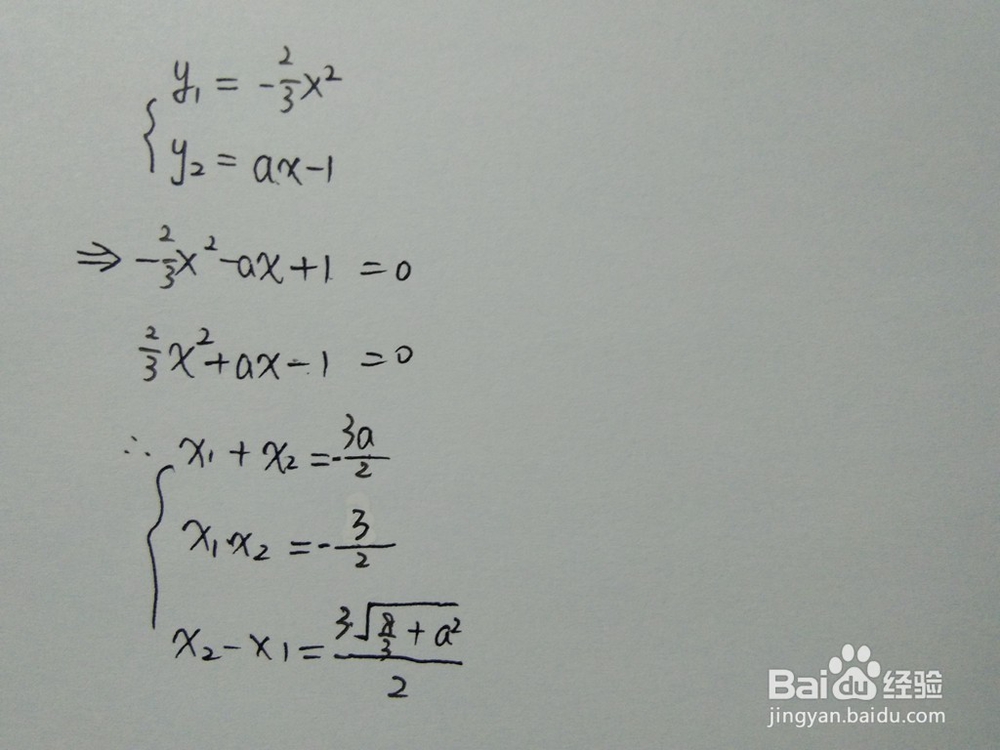
2、通过定积分,求围成面积通式如下:
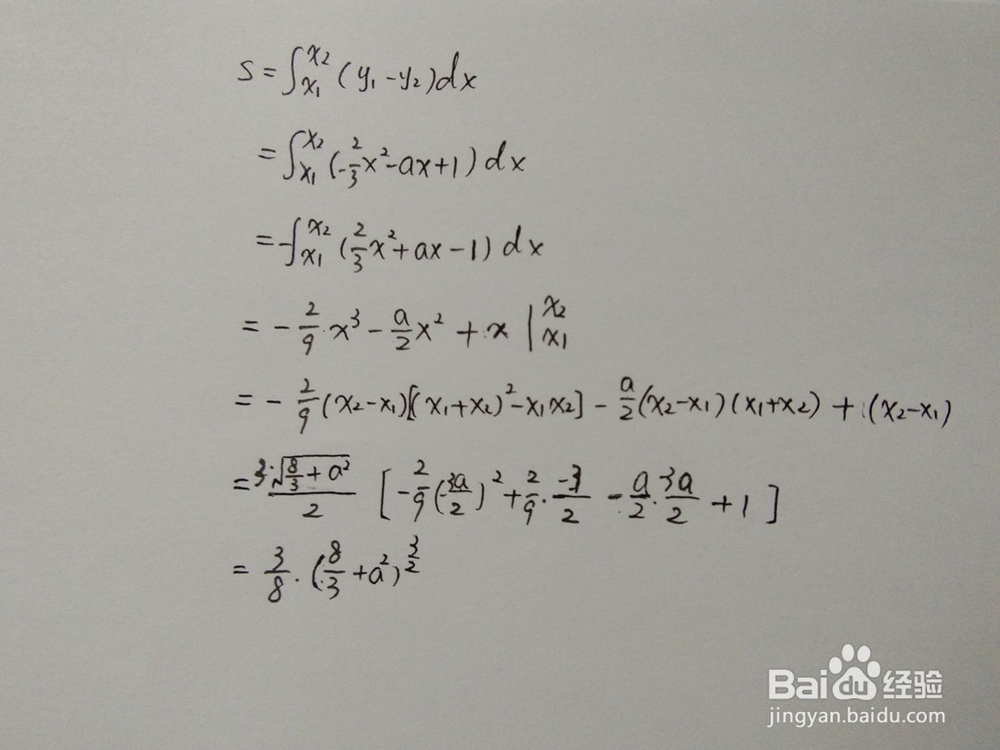
2.当a=0时
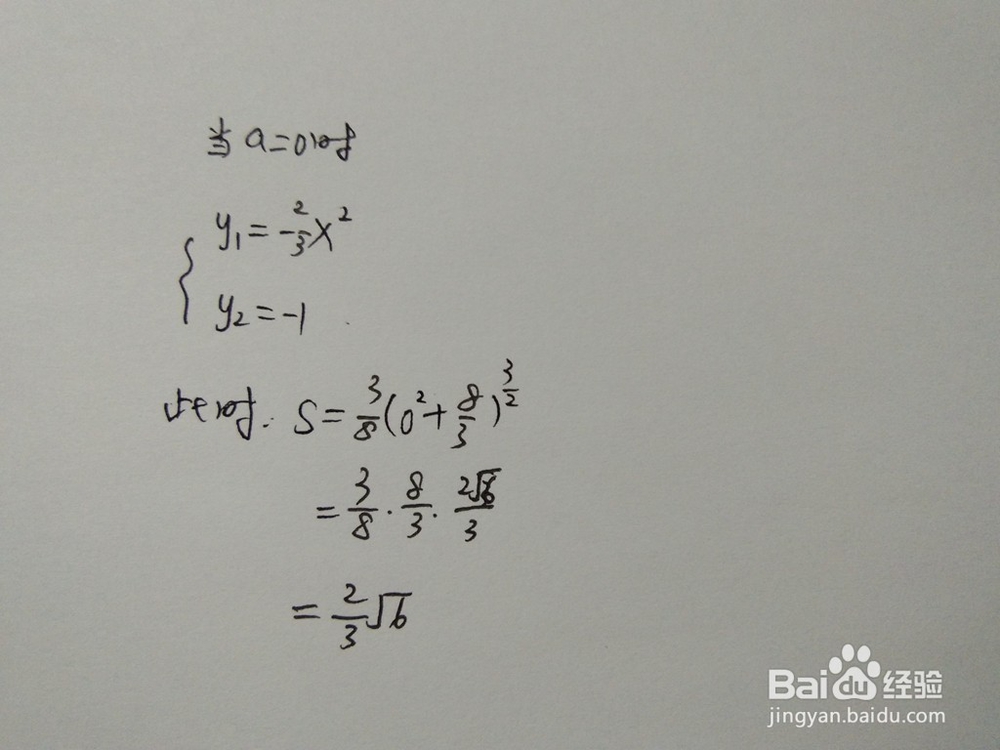
3.当a=1/3时
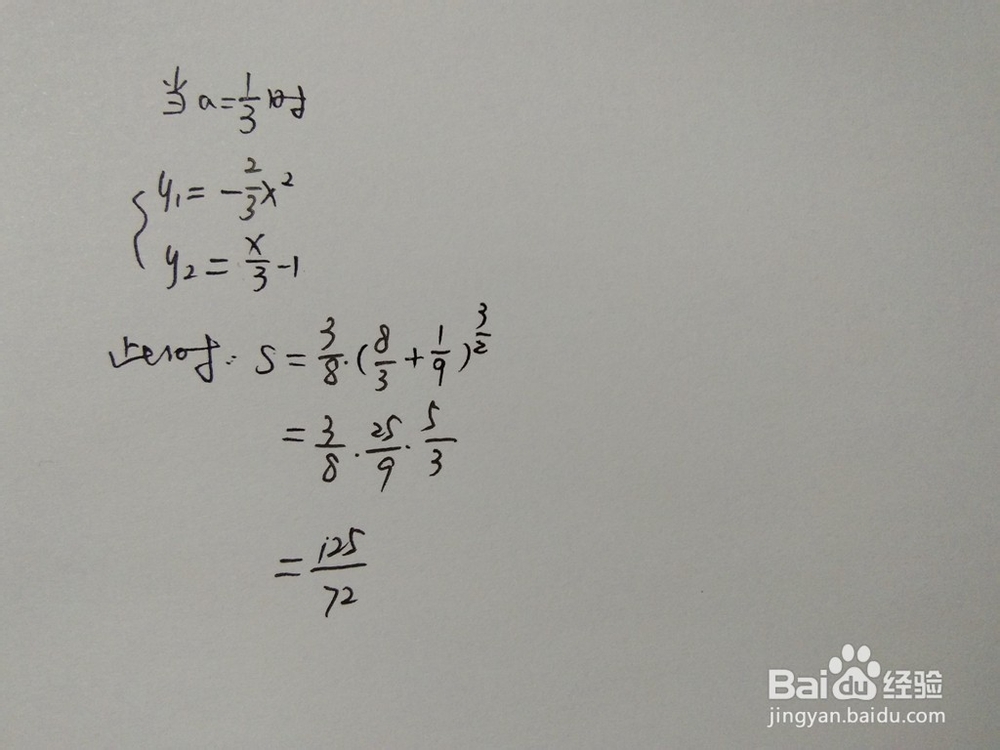
4.当a=1/2时

5.当a=1时