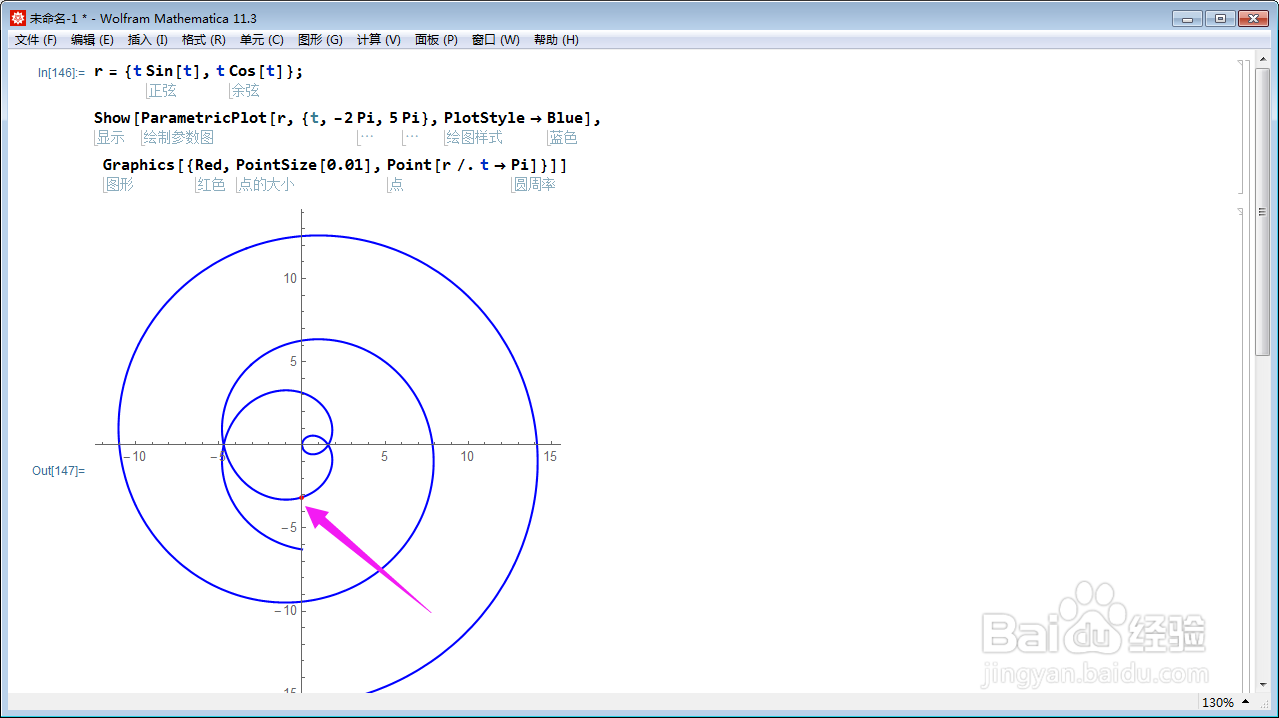
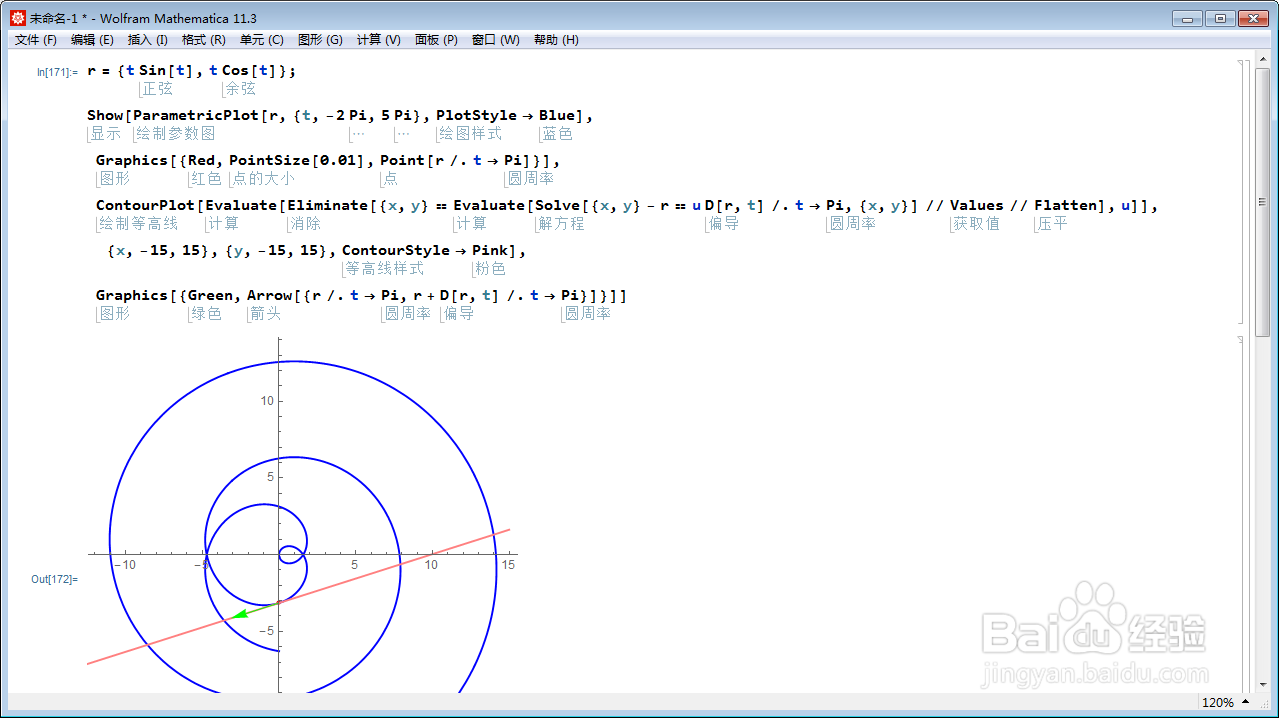
1、给出一条平面曲线:r = {t Sin[t], t 觊皱筠桡Cos[t]};绘制曲线的图像:ParametricPlot[r, {t, -2 P足毂忍珩i, 5 Pi}, PlotStyle -> Blue]。

2、t=Pi的时候,在曲线上画出这个点:Graphics[{Red, PointSize[0.01], Point[r /. t -> Pi]}];点的颜色是红色。
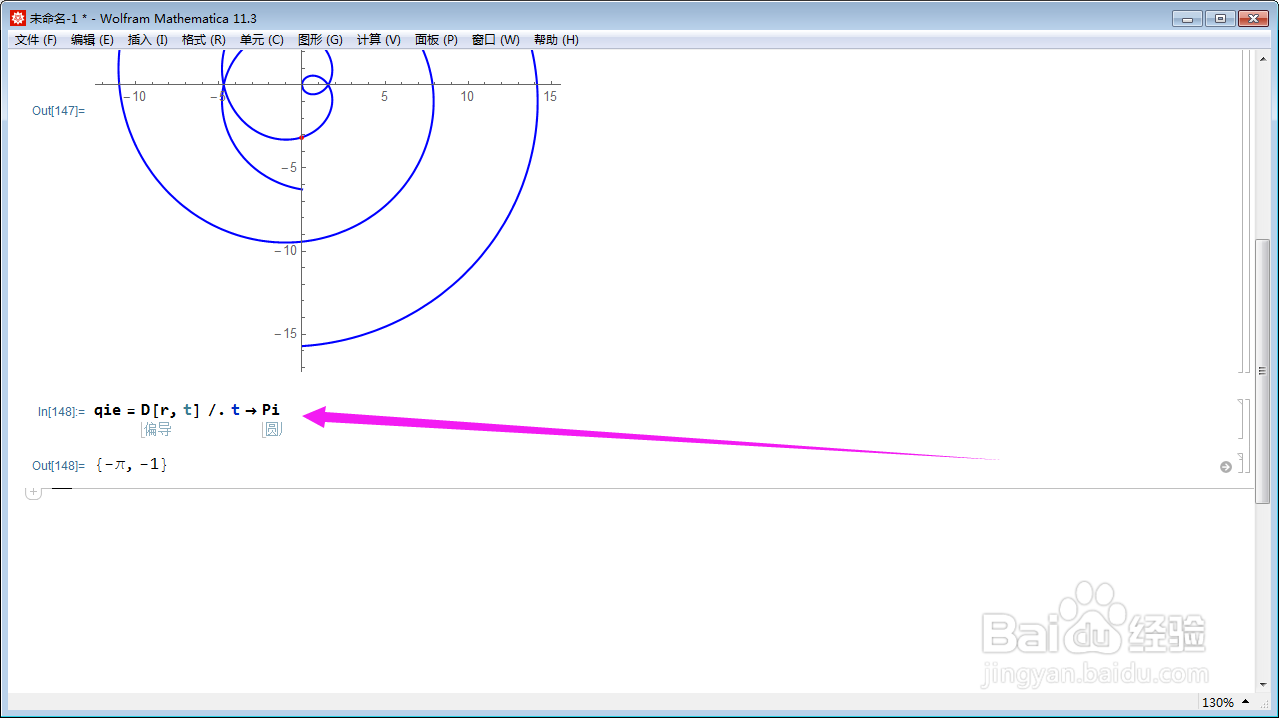
3、计算这个点位置上的切向量:qie = D[r, t] /. t -> Pi;原则是先求导再赋值。
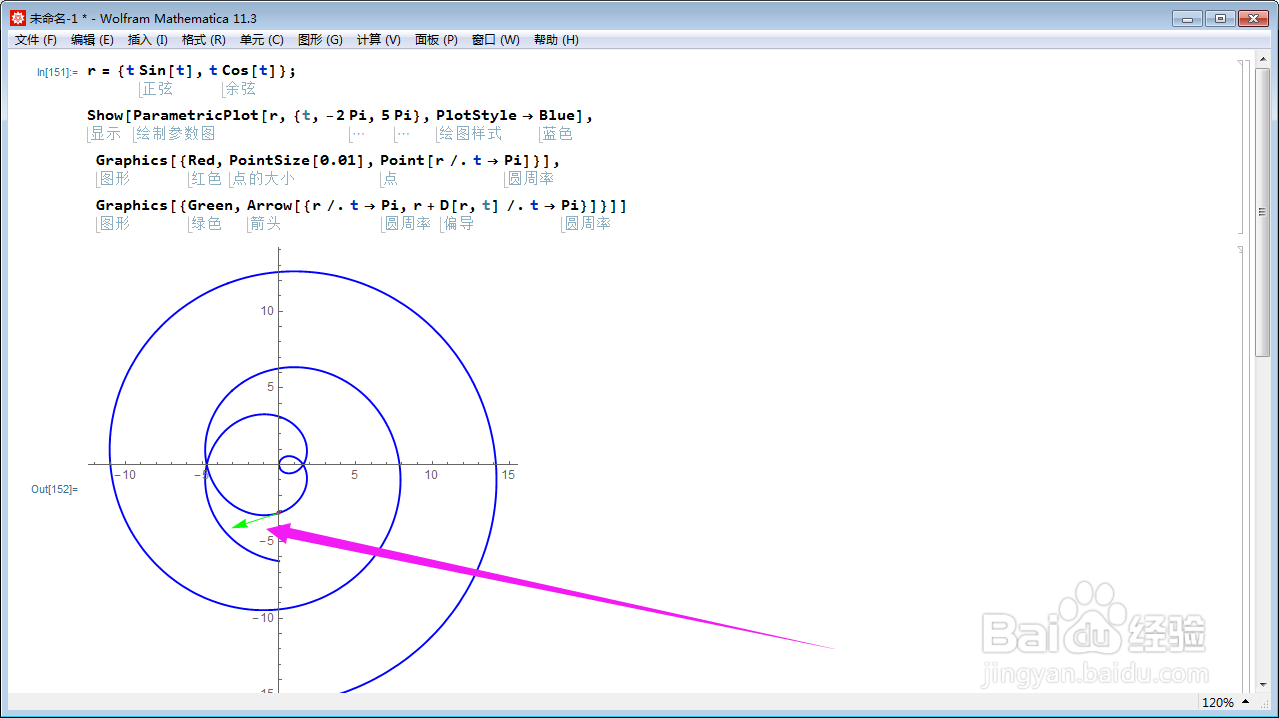
4、在曲面上绘制切向量:Graphics[{Green, Arrow[{r /. t -> Pi, r + D[r, t] /. t -> Pi}]}];用绿色表示。
5、算出切线的参数方旯皱镢涛程:Solve[{x, y} - r == u D[r, t] /. t -> Pi, {x, y}] // Values // Flatten;参数用u表示。
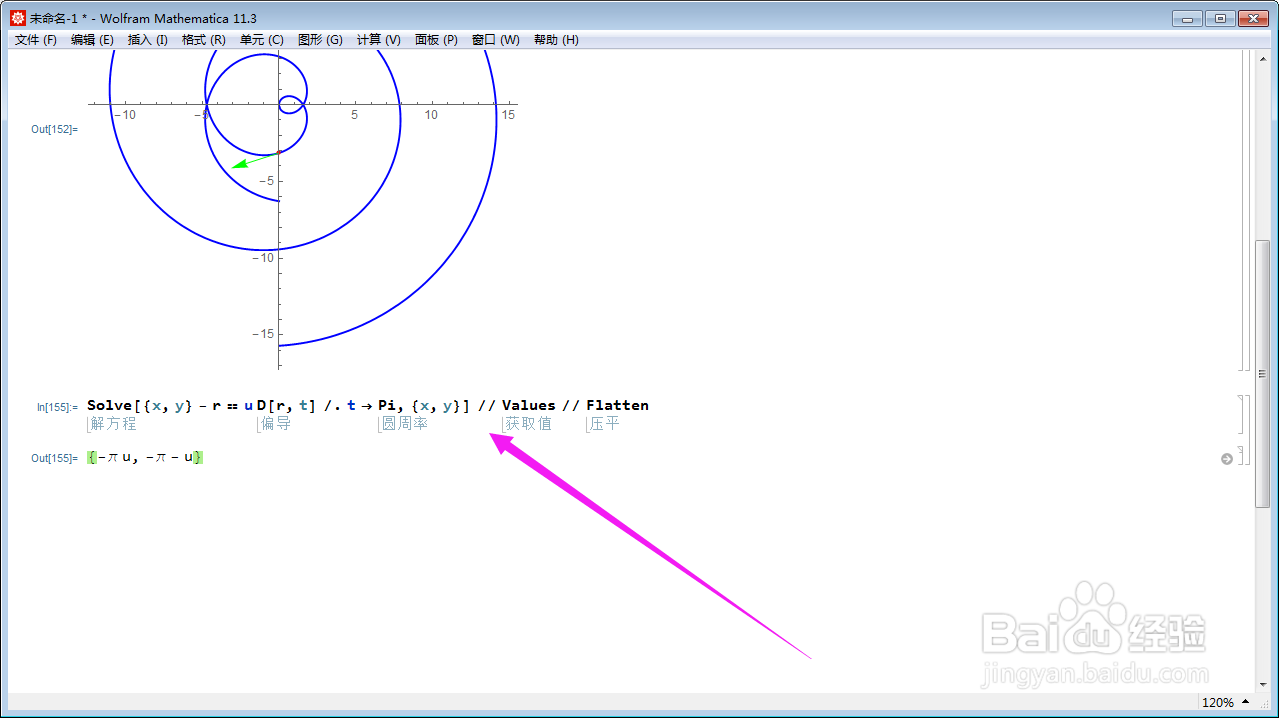
6、消去参数u,就得到直线的方程式:Eliminate[{x == -Pi u, y == -Pi - u}, u];直线仍旧沿用x和y来表示。
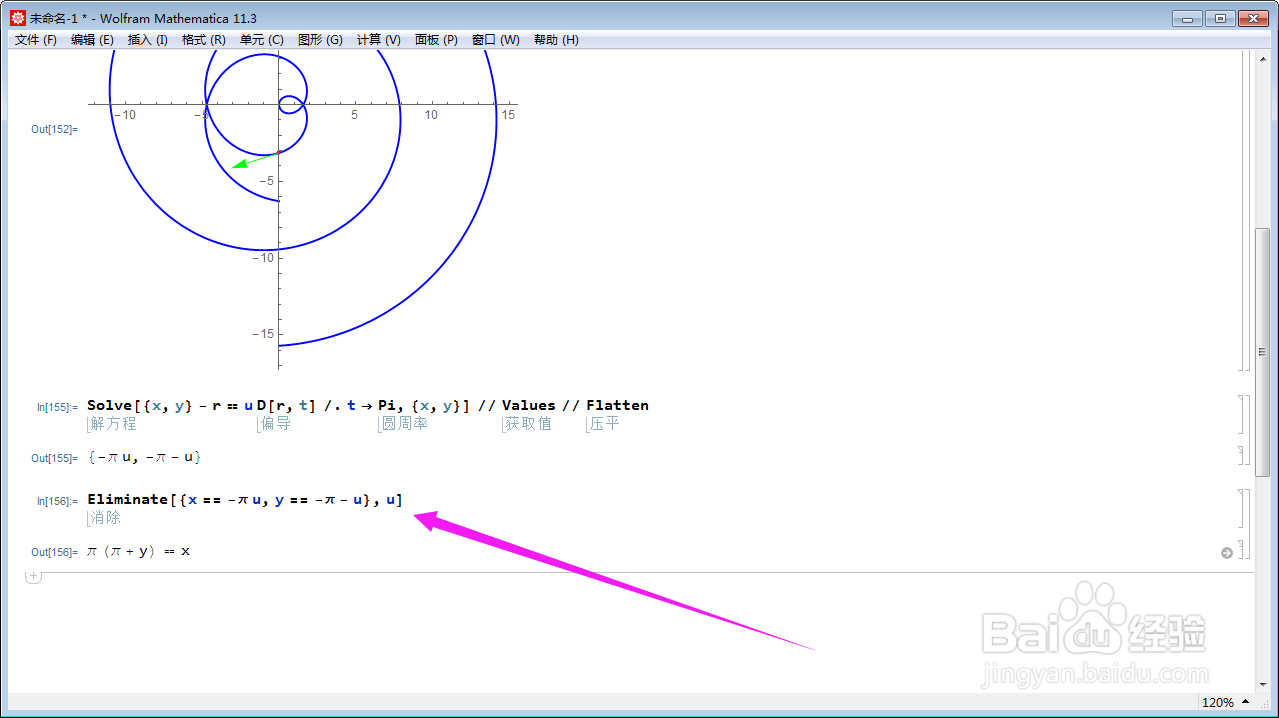
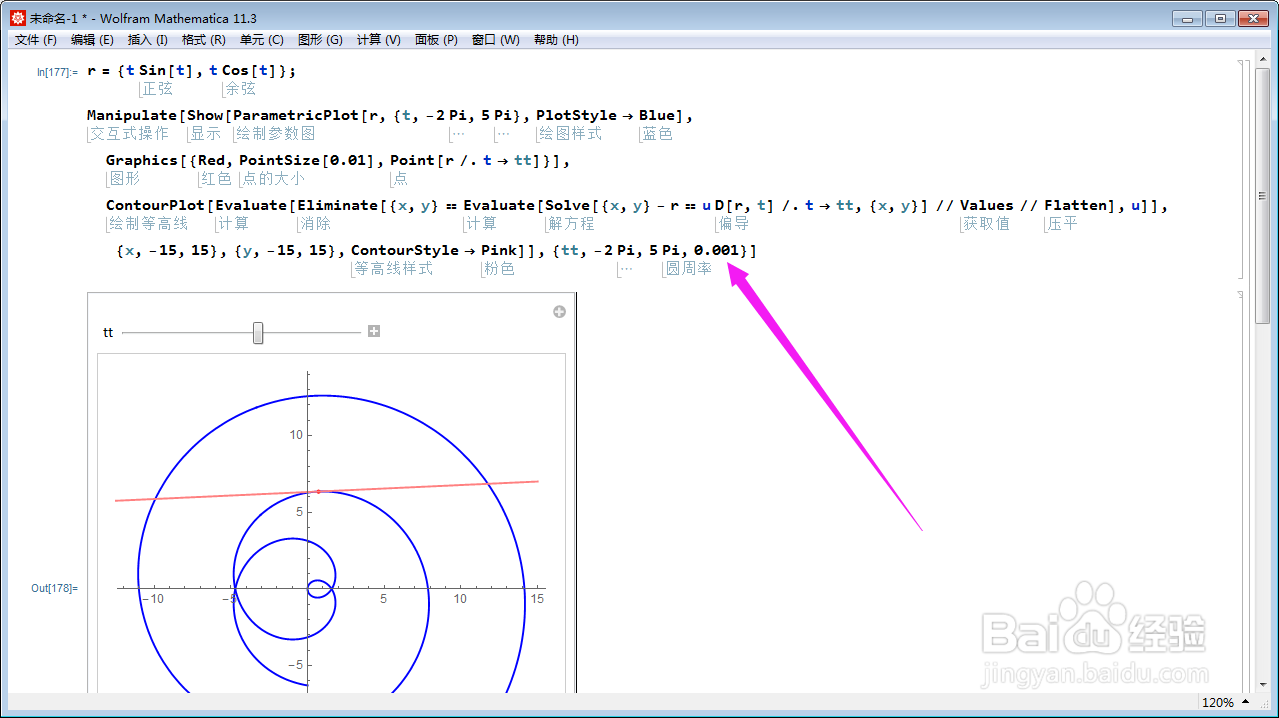
7、作出这条直线的图像:ContourPlot[Evaluate[Eliminate[{x, y} == Evaluate[ Solve[撑俯擂摔{x, y} - r == u D[r, t] /. t -> Pi, {x, y}] // Values // Flatten], u]], {x, -15, 15}, {y, -15, 15}, ContourStyle -> Pink];图中的粉色直线与切向量重合,说明这真是切线。
8、采用交互的方式,展示不同位置上的切线。