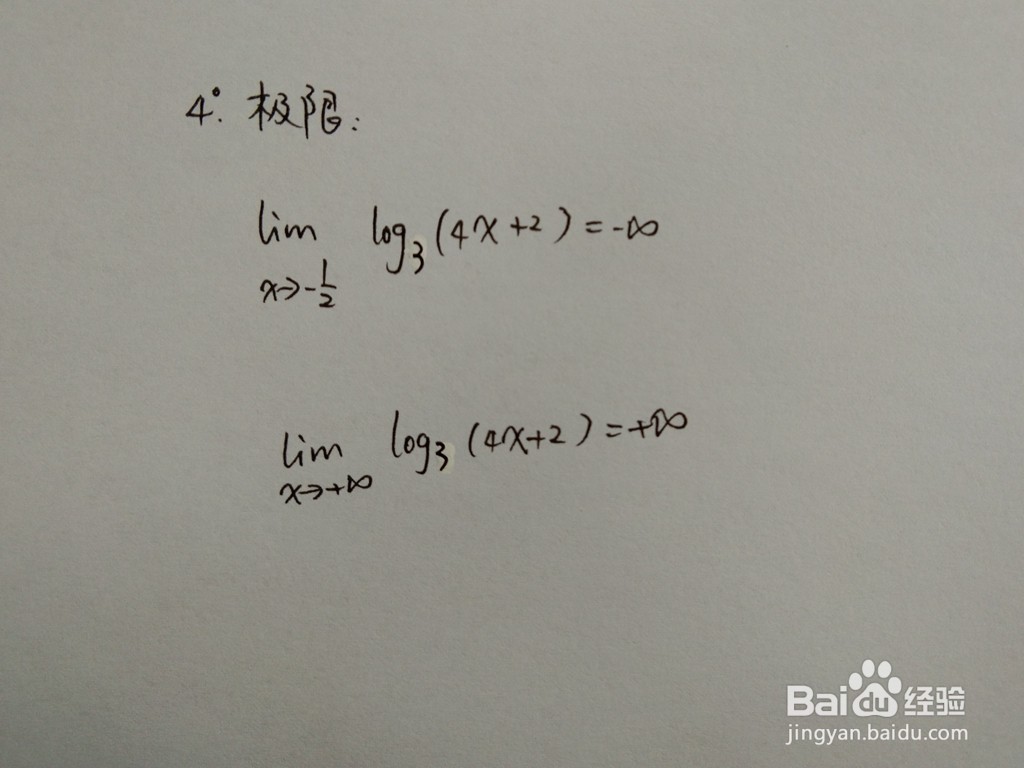1、对于本题为对数函数,即要求真数部分为正数,进而可求出函数的定义域。

2、函数的单调性,通过函数的一阶导数,求出函数的单调区间。
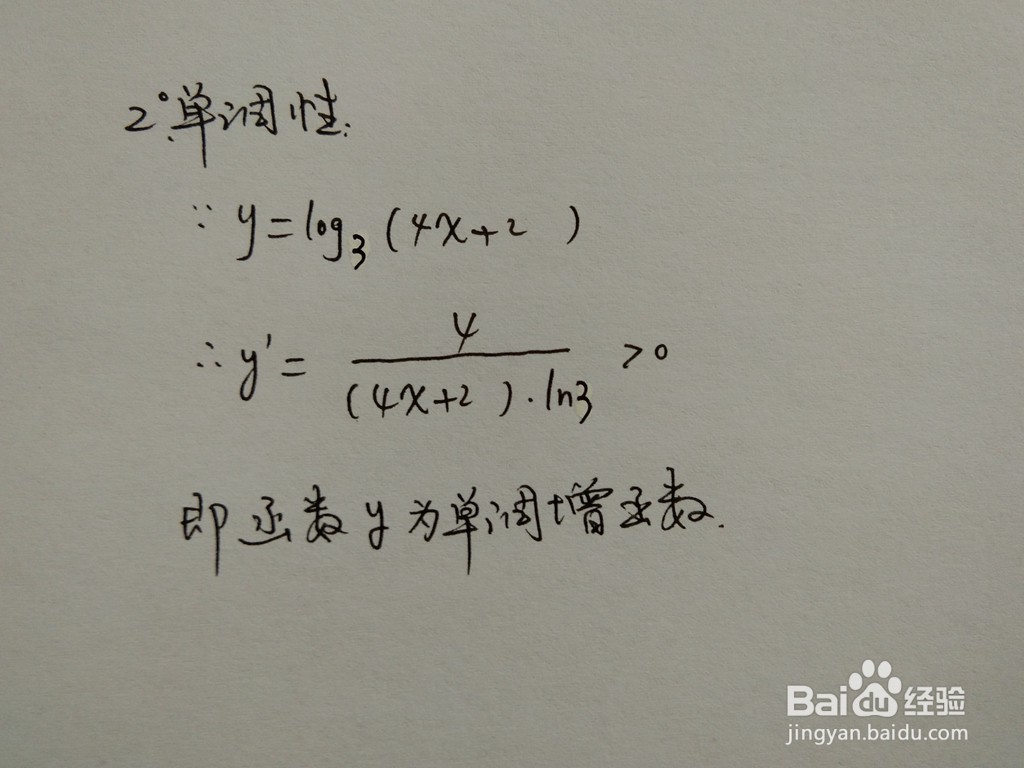
3、根据函数的二阶导数,判断函数的凸凹性,进而可得函数的凸凹区间。
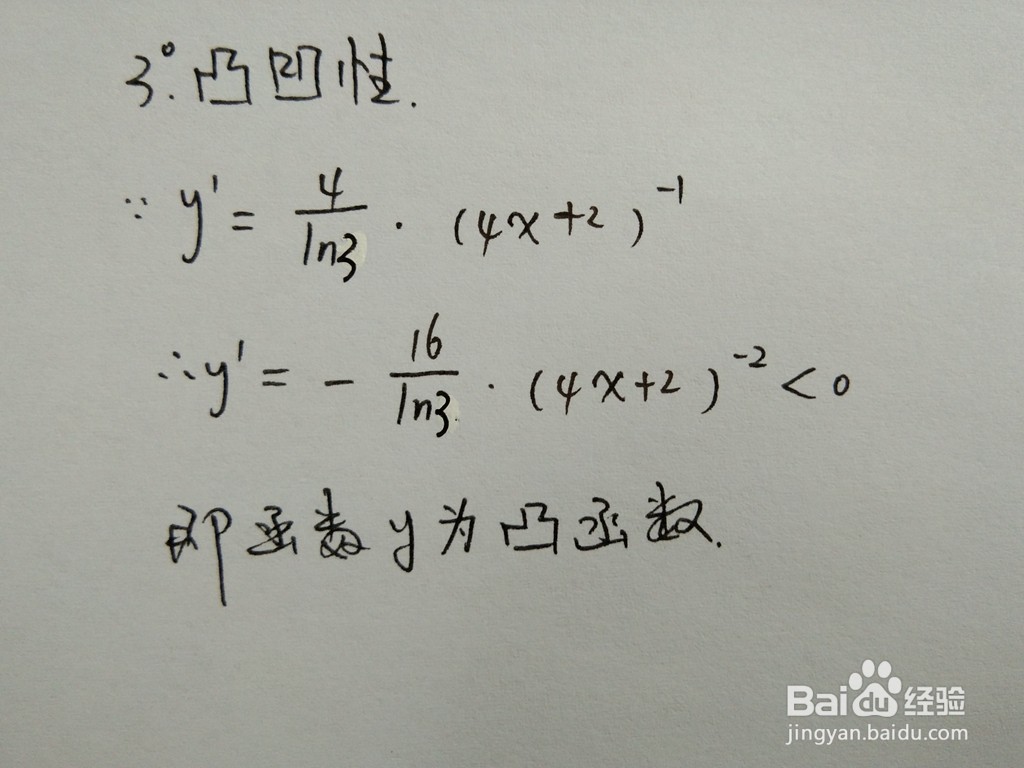
4、如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
5、函数在间断点处的极限:
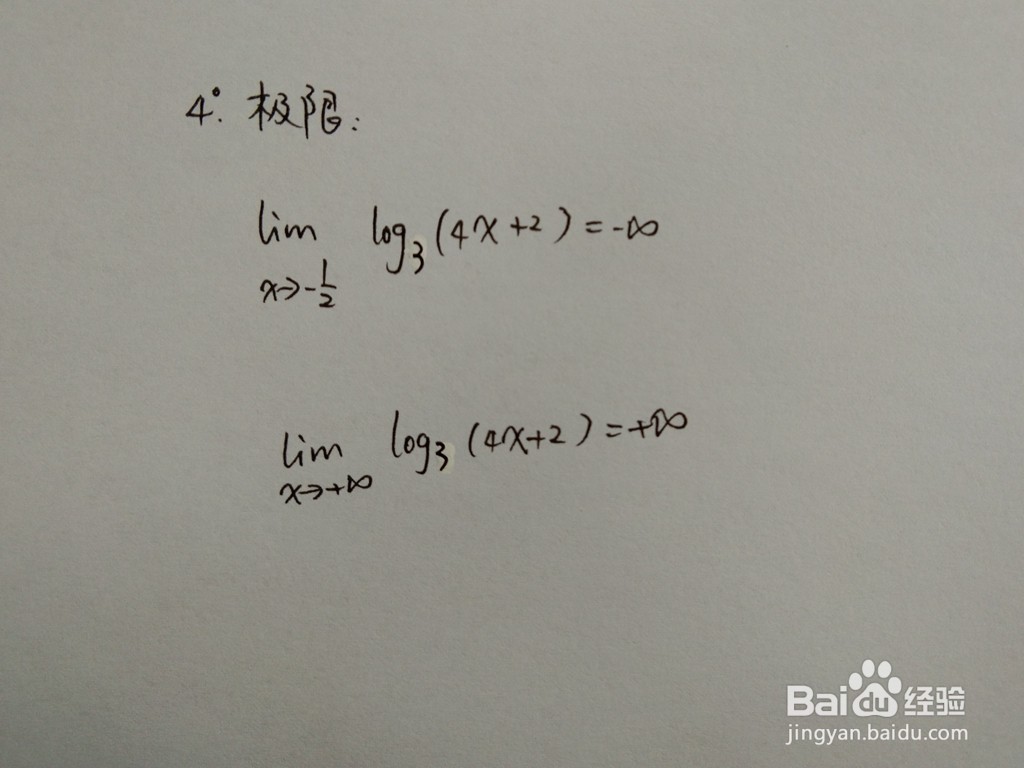
时间:2026-02-15 21:35:48
1、对于本题为对数函数,即要求真数部分为正数,进而可求出函数的定义域。

2、函数的单调性,通过函数的一阶导数,求出函数的单调区间。
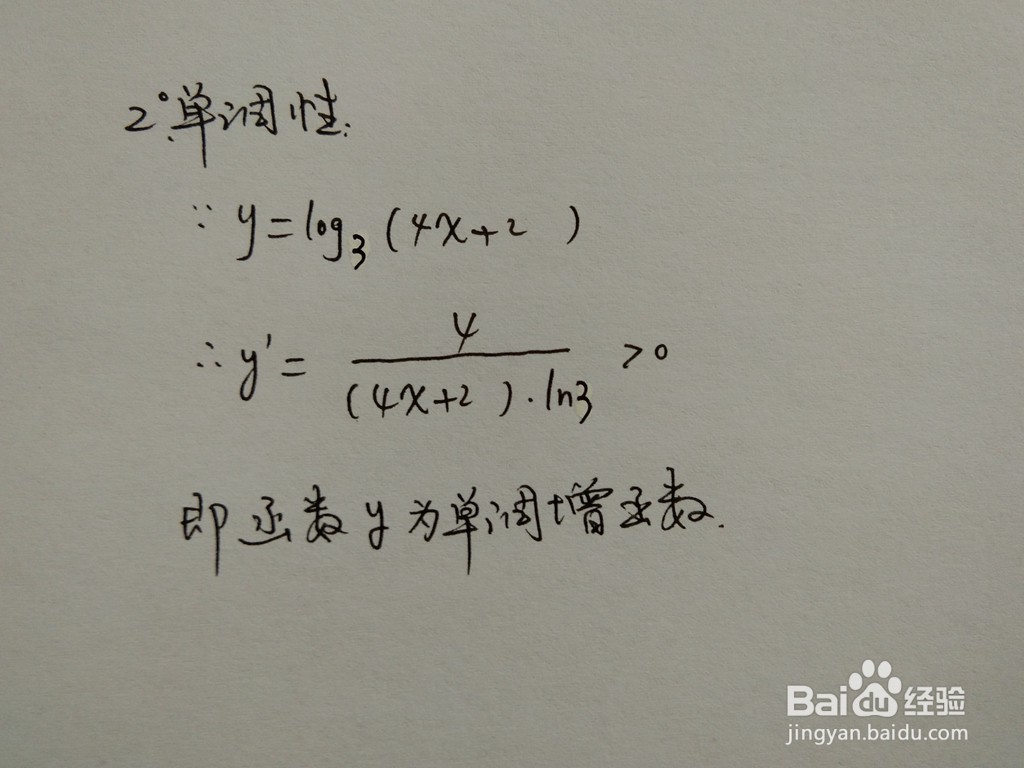
3、根据函数的二阶导数,判断函数的凸凹性,进而可得函数的凸凹区间。
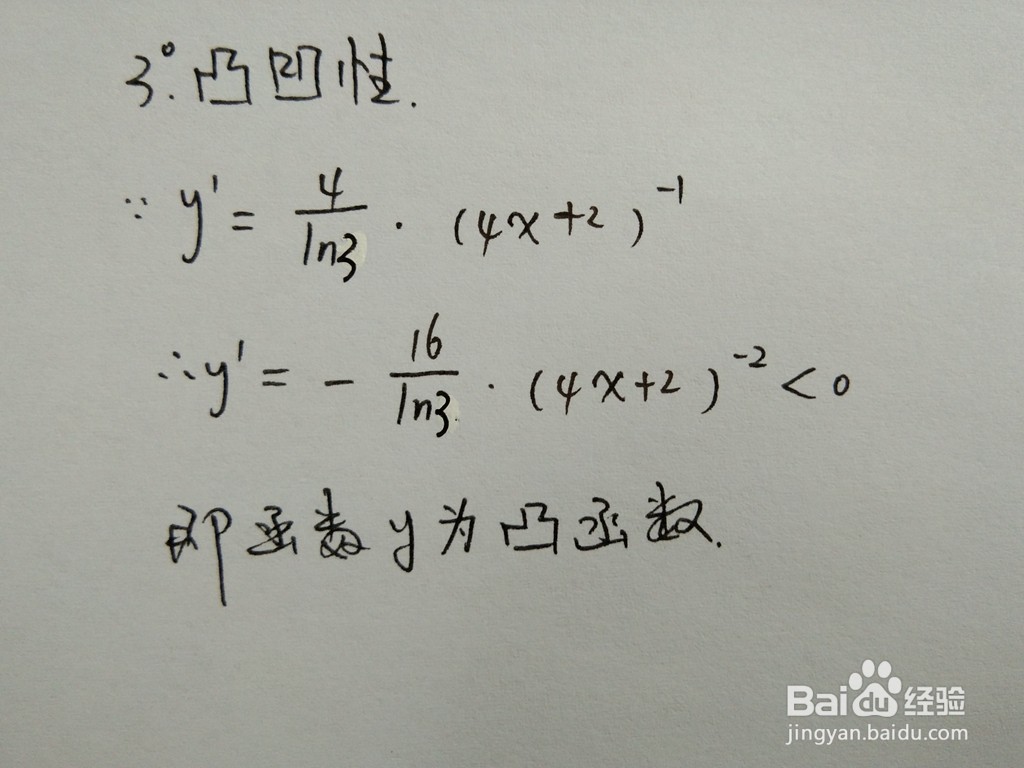
4、如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
5、函数在间断点处的极限: